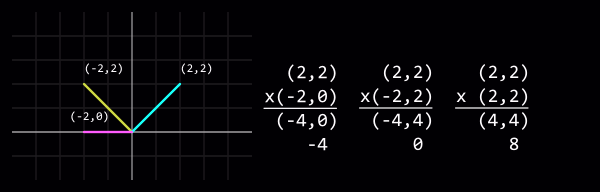Ru/Vector: Difference between revisions
(Created page with "{{lang|Vector:ru|Вектор}} {{toc-right}} '''<code>Вектор</code>''' это C++ класс который представляет направление и име...") |
mNo edit summary |
||
| (10 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{LanguageBar|title = Вектор (Vector)}} | ||
{{translate}} | |||
{{toc-right}} | {{toc-right}} | ||
'''<code> | '''<code>Vector</code>''' это C++ класс, который представляет направление и длину отрезка прямой, начинающегося в {{L|origin|точке отсчёта}}. | ||
== Оси == | |||
Каждый вектор содержит три <code>{{L|vec_t}}</code> координаты: | |||
;X | |||
:+вперёд/-назад | |||
;Y | |||
:+влево/-вправо | |||
;Z | |||
:+вверх/-вниз | |||
<code>(1,20,5)</code> означает 1 {{L|unit|единица}} вперёд, 20 единиц влево и 5 единиц вверх. | |||
== | {{Note|Класс вектора в движке Source является геометрическим понятием и сильно отличается от вектора из [[Wikipedia:Vector (C++)|STL]], который является массивом [[Wikipedia:Array|массивом]]. STL вектор в коде движка был переименован в <code>{{L|CUtlVector}}</code>.}} | ||
== Объявление == | |||
Vector vecMyVector = Vector(1,20,5); | Vector vecMyVector = Vector(1,20,5); | ||
* | * Класс вектора пишется как <code>Vector</code>, а не vector. | ||
* | * Вы можете определять значения X, Y и Z отдельно. | ||
* | * Префикс <code>vec</code> (или просто <code>v</code>) определяет переменную как вектор. | ||
== | == Направление == | ||
У вектора нет направления; это определяется кодом, который используется. | |||
In the vast majority of cases a vector will be interpreted as '''world axis aligned''' regardless of an entity's rotation, but there are few cases (e.g. applying physics forces), where they are considered '''object axis aligned'''. | In the vast majority of cases a vector will be interpreted as '''world axis aligned''' regardless of an entity's rotation, but there are few cases (e.g. applying physics forces), where they are considered '''object axis aligned'''. | ||
| Line 29: | Line 36: | ||
There is no way of telling which interpretation will be used from the variable, so check for function comments when in doubt. Use [[#Helper functions|<code>VectorRotate()</code>]] and [[#Helper functions|<code>VectorIRotate()</code>]] to translate between alignments. | There is no way of telling which interpretation will be used from the variable, so check for function comments when in doubt. Use [[#Helper functions|<code>VectorRotate()</code>]] and [[#Helper functions|<code>VectorIRotate()</code>]] to translate between alignments. | ||
== | == Использование == | ||
; | ; Позиционирование | ||
: Every entity's position ('origin') is stored as a vector relative to its | : Every entity's position ('origin') is stored as a vector relative to its {{L|parent}}: you are likely to be familiar with this idea already as {{L|coordinates|Cartesian grid coordinates}}. See <code>{{L|GetAbsOrigin()}}</code> for more details. | ||
; | ; Движение | ||
: An entity attempts to move the length of its | : An entity attempts to move the length of its {{L|velocity}} vector once per second. | ||
; | ; Траектории столкновений | ||
: A | : A {{L|UTIL_TraceLine|Traceline}} or {{L|UTIL_TraceHull|-hull}} is fired from one point to another, detecting what it "hits" along its path. | ||
== | == Операции == | ||
Чтобы результат имел смысл, все векторы в операции должны иметь общую {{L|origin|точку отсчёта}}. Используется ли локальное или абсолютное начало отсчета, зависит от того, чего вы пытаетесь достичь. | |||
=== | === Сложение === | ||
Сложение двух (или более) векторов '''складывает''' их значения. Вы уже складывали векторы, если толкали что либо двумя руками! | |||
[[File:Vector_add.png|center| | [[File:Vector_add.png|center|Сложение векторов: (4,1) + (-3,1) = (1,2)]] | ||
=== | === Вычитание === | ||
Вычитание одного вектора из другого это '''разница''' между ними - другими словами, как добраться из первого вектора в другой. | |||
[[File:Vector_subtraction.png|center| | [[File:Vector_subtraction.png|center|Вычитание векторов: (2,3) - (-2,1) = (4,2)]] | ||
{{tip| | {{tip|От порядка векторов зависит направление получившегося вектора}} | ||
=== | === Умножение(произведение) === | ||
==== | ==== Скалярное ==== | ||
Умножение или деление вектора [[Wikipedia:Scalar|скалярно]] (то есть на {{L|int}} или {{L|float}}) изменит '''длину''' вектора не изменяя его направления. | |||
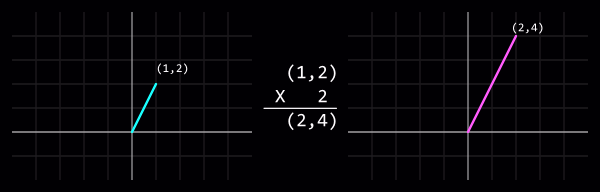
[[File:Vector-scalar_multiply.png|center| | [[File:Vector-scalar_multiply.png|center|Скалярное произведение векторов: (1,2) x 2 = (2,4)]] | ||
{{tip| | {{tip|Делениние вектора на его длину {{L|normal|нормирует}} его. Используйте <code>VectorNormalize()</code> чтобы быстро это сделать.}} | ||
==== | ==== Нормированное скалярное ==== | ||
Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been | Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been {{L|normal}}ised is equal to the '''cosine''' of the angle between the two vectors. | ||
One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed. | One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed. | ||
{{note|''True dot products are only produced when the length of both vectors is 1.'' The | {{note|''True dot products are only produced when the length of both vectors is 1.'' The {{L|normal}}isation step has been skipped in the following demonstration to make its equations simpler (but the positive/zero/negative rule still applies).}} | ||
[[File:Vector_dotproduct.png|center| | [[File:Vector_dotproduct.png|center|Принцип вычисления нормированного скалярное произведения: (2,2) x (-2,0) = (-4,0) = -4; (2,2) x (-2,2) = (-4,4) = 0; (2,2) x (2,2) = (4,4) = 8]] | ||
Этот код вычисляет скалярное произведение с помощью различных вспомогательных функций Source: | |||
<source lang=cpp> | <source lang=cpp> | ||
| Line 93: | Line 100: | ||
{{tip|There is no need to normalise if you only care about whether one location is in front of another.}} | {{tip|There is no need to normalise if you only care about whether one location is in front of another.}} | ||
==== | In this code, the expression {{code|dot > 0}} is true if the angle between the input vectors is < 90°. If you need two vectors to be < x degrees apart, then {{code|dot > cos(x°)}} must be true, where cos(x°) is a constant. Note that this way, the dot product allows to check the angle between two vectors without calling the rather expensive cosine function at runtime. | ||
{{important|1=There are various entities with keyvalues denoting a maximum angle as a float in the range -1.0 to 1.0, for example the <tt>FieldOfView</tt> keyvalue of {{ent|trigger_look}}. Such a keyvalue commonly refers to a dot product, which means that it is <b style=white-space:nowrap>not a linear</b> function of the desired angle. A common mistake would be to set it to a value of 0.5 which is intended to correspond to an angle of 45°, but instead, the correct value would be cos(45°) ≈ 0.707!}} | |||
{| class=wikitable | |||
!style=background:#333| Угол между векторами | |||
| x° || cos<sup>-1</sup>(<tt>dot</tt>) || 0° || 1° || 2° || 5° || 10° || 15° || 30° || 45° || 60° || 75° || 90° || 120° || 180° | |||
|- | |||
!style=background:#333| Нормированное скалярное произведение | |||
| cos(x°) || <tt>dot</tt> || 1.0 || 0.99985 || 0.99939 || 0.99619 || 0.98481 || 0.96593 || 0.86603 || 0.70711 || 0.5 || 0.25882 || 0 || -0.5 || -1.0 | |||
|} | |||
==== Векторное ==== | |||
A cross product is a vector '''perpendicular''' to two input vectors. It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis. | A cross product is a vector '''perpendicular''' to two input vectors. It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis. | ||
| Line 99: | Line 118: | ||
The equation is fiddly and doesn't have to be learnt; just use <code>CrossProduct(vecA,vecB,&vecResult)</code>. There generally isn't any need to normalise the input vectors. Most modders will likely only use cross products rarely, if ever - but if required, be aware that a [http://mathworld.wolfram.com/CrossProduct.html moderate amount of math] is required to [[Wikipedia:Cross product|properly understand]] this operation. | The equation is fiddly and doesn't have to be learnt; just use <code>CrossProduct(vecA,vecB,&vecResult)</code>. There generally isn't any need to normalise the input vectors. Most modders will likely only use cross products rarely, if ever - but if required, be aware that a [http://mathworld.wolfram.com/CrossProduct.html moderate amount of math] is required to [[Wikipedia:Cross product|properly understand]] this operation. | ||
== | == Поворот == | ||
Для поворота вектора нужна {{L|matrix3x4_t|матрица}}, это нельзя сделать также легко как умножение. К счастью не нужно в это вникать: можно просто вызвать <code>VectorRotate(Vector in, QAngle in, Vector& out)</code>. | |||
== | == Специальные вектора == | ||
Source | в Source есть два вида специальных векторов: | ||
; <code>vec3_origin</code> | ; <code>vec3_origin</code> | ||
: Vector(0,0,0). | : Vector(0,0,0). | ||
; <code>vec3_invalid</code> | ; <code>vec3_invalid</code> | ||
: | : Это используется для недопустимых векторов, например, если результатом функцим станет вектор к точке на пересечении двух параллельных прямых. | ||
== | == Функции пользователя == | ||
=== | === Длина === | ||
; <code> | ; <code>{{L|vec_t}} Length()</code> | ||
; <code>vec_t LengthSqr()</code> | ; <code>vec_t LengthSqr()</code> | ||
: <code>Length()</code> returns the vector's length in | : <code>Length()</code> returns the vector's length in {{L|unit}}s. It's faster to use <code>LengthSqr()</code> and square the other value being compared. | ||
; <code> | ; <code>{{L|boolean|bool}} IsLengthGreaterThan(flValue)</code> | ||
; <code>bool IsLengthLessThan(flValue)</code> | ; <code>bool IsLengthLessThan(flValue)</code> | ||
: Helpers that perform fast length checks using <code>LengthSqr()</code>. | : Helpers that perform fast length checks using <code>LengthSqr()</code>. | ||
| Line 124: | Line 143: | ||
: Sets all elements to 0. | : Sets all elements to 0. | ||
=== | === Направление === | ||
; <code>void Init(vec_t X, Y, Z)</code> | ; <code>void Init(vec_t X, Y, Z)</code> | ||
| Line 136: | Line 155: | ||
: Clamps the vector's ordinates either above or below the given values. The ordinates won't stay in proportion (i.e. direction might change). | : Clamps the vector's ordinates either above or below the given values. The ordinates won't stay in proportion (i.e. direction might change). | ||
=== | === Сравнение === | ||
; <code>vec_t DistTo(vOther)</code> | ; <code>vec_t DistTo(vOther)</code> | ||
| Line 148: | Line 167: | ||
: Tests whether the Vector ends within the given box. Box min/max values are local to the Vector. | : Tests whether the Vector ends within the given box. Box min/max values are local to the Vector. | ||
=== | === Приведение === | ||
; <code>Vector2D AsVector2D()</code> | ; <code>Vector2D AsVector2D()</code> | ||
: Casts to | : Casts to {{L|Vector2D}}. | ||
; <code>vec_t Length2D()</code> | ; <code>vec_t Length2D()</code> | ||
; <code>vec_t Length2DSqr()</code> | ; <code>vec_t Length2DSqr()</code> | ||
: As their standard equivalents, but ignoring the Z-axis. | : As their standard equivalents, but ignoring the Z-axis. | ||
; <code>Base()</code> | ; <code>Base()</code> | ||
: Casts to | : Casts to {{L|vec_t}}*, basically the same as &vec.x or (float*)&vec. | ||
== | == Вспомогательные функции == | ||
These globals are all available through <code>cbase.h</code>. | These globals are all available through <code>cbase.h</code>. | ||
; <code> | ; <code>{{L|float}} VectorNormalize(vec)</code> | ||
: Divides the vector by its length, | : Divides the vector by its length, {{L|normal}}ising it. Modifies the Vector and returns the old length. | ||
; <code> | ; <code>{{L|vec_t}} DotProduct(vecA,vecB)</code> | ||
: See [[#Dot product]]. | : See [[#Dot product]]. | ||
; <code>void CrossProduct(vecA,vecB,vecResult)</code> | ; <code>void CrossProduct(vecA,vecB,vecResult)</code> | ||
: See [[#Cross product]]. | : See [[#Cross product]]. | ||
; <code>void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)</code> | ; <code>void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)</code> | ||
: See | : See {{L|matrix3x4_t}}. | ||
* | * {{L|UTIL_VecToYaw()|<code>UTIL_VecToYaw()</code> / <code>UTIL_VecToPitch()</code>}} | ||
* | * {{L|AngleVectors()|<code>AngleVectors()</code> / <code>VectorAngles()</code>}} | ||
== | == Смотри также == | ||
* [[Wikipedia:Euclidean vector]] | * [[Wikipedia:Euclidean vector]] | ||
* <code> | * <code>{{L|vec_t}}</code> | ||
* <code> | * <code>{{L|Vector2D}}</code> | ||
* <code> | * <code>{{L|QAngle}}</code> | ||
* <code> | * <code>{{L|matrix3x4_t}}</code> | ||
* <code> | * <code>{{L|CUtlVector}}</code> | ||
{{ACategory|Source class}} | |||
{{ACategory|Helpers}} | |||
{{ACategory|Glossary}} | |||
{{ACategory|Variables}} | |||
{{ACategory|Helpers}} | |||
Latest revision as of 13:20, 27 May 2025
This page either contains information that is only partially or incorrectly translated, or there isn't a translation yet.
If this page cannot be translated for some reason, or is left untranslated for an extended period of time after this notice is posted, the page should be requested to be deleted.
Also, please make sure the article complies with the alternate languages guide.
Vector это C++ класс, который представляет направление и длину отрезка прямой, начинающегося в точке отсчёта.
Оси
Каждый вектор содержит три vec_t координаты:
- X
- +вперёд/-назад
- Y
- +влево/-вправо
- Z
- +вверх/-вниз
(1,20,5) означает 1 единица вперёд, 20 единиц влево и 5 единиц вверх.
CUtlVector.Объявление
Vector vecMyVector = Vector(1,20,5);
- Класс вектора пишется как
Vector, а не vector. - Вы можете определять значения X, Y и Z отдельно.
- Префикс
vec(или простоv) определяет переменную как вектор.
Направление
У вектора нет направления; это определяется кодом, который используется.
In the vast majority of cases a vector will be interpreted as world axis aligned regardless of an entity's rotation, but there are few cases (e.g. applying physics forces), where they are considered object axis aligned.
There is no way of telling which interpretation will be used from the variable, so check for function comments when in doubt. Use VectorRotate() and VectorIRotate() to translate between alignments.
Использование
- Позиционирование
- Every entity's position ('origin') is stored as a vector relative to its parent: you are likely to be familiar with this idea already as Cartesian grid coordinates. See
GetAbsOrigin()for more details. - Движение
- An entity attempts to move the length of its velocity vector once per second.
- Траектории столкновений
- A Traceline or -hull is fired from one point to another, detecting what it "hits" along its path.
Операции
Чтобы результат имел смысл, все векторы в операции должны иметь общую точку отсчёта. Используется ли локальное или абсолютное начало отсчета, зависит от того, чего вы пытаетесь достичь.
Сложение
Сложение двух (или более) векторов складывает их значения. Вы уже складывали векторы, если толкали что либо двумя руками!
Вычитание
Вычитание одного вектора из другого это разница между ними - другими словами, как добраться из первого вектора в другой.
Умножение(произведение)
Скалярное
Умножение или деление вектора скалярно (то есть на int или float) изменит длину вектора не изменяя его направления.
VectorNormalize() чтобы быстро это сделать.Нормированное скалярное
Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been normalised is equal to the cosine of the angle between the two vectors.
One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed.
Этот код вычисляет скалярное произведение с помощью различных вспомогательных функций Source:
Vector vecTarget = pTarget->GetAbsOrigin() - GetAbsOrigin(); // Get local vector to target
VectorNormalize(vecTarget); // Normalisation needs to be done beforehand
Vector vecFacing;
AngleVectors(GetLocalAngles(),&vecFacing); // Convert facing angle to equivalent vector (arrives normalised)
float result = DotProduct(vecTarget,vecFacing); // Get the dot product
if (result > 0)
Msg("pTarget is in front of me!\n");
In this code, the expression dot > 0 is true if the angle between the input vectors is < 90°. If you need two vectors to be < x degrees apart, then dot > cos(x°) must be true, where cos(x°) is a constant. Note that this way, the dot product allows to check the angle between two vectors without calling the rather expensive cosine function at runtime.
| Угол между векторами | x° | cos-1(dot) | 0° | 1° | 2° | 5° | 10° | 15° | 30° | 45° | 60° | 75° | 90° | 120° | 180° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Нормированное скалярное произведение | cos(x°) | dot | 1.0 | 0.99985 | 0.99939 | 0.99619 | 0.98481 | 0.96593 | 0.86603 | 0.70711 | 0.5 | 0.25882 | 0 | -0.5 | -1.0 |
Векторное
A cross product is a vector perpendicular to two input vectors. It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis.
The equation is fiddly and doesn't have to be learnt; just use CrossProduct(vecA,vecB,&vecResult). There generally isn't any need to normalise the input vectors. Most modders will likely only use cross products rarely, if ever - but if required, be aware that a moderate amount of math is required to properly understand this operation.
Поворот
Для поворота вектора нужна матрица, это нельзя сделать также легко как умножение. К счастью не нужно в это вникать: можно просто вызвать VectorRotate(Vector in, QAngle in, Vector& out).
Специальные вектора
в Source есть два вида специальных векторов:
vec3_origin- Vector(0,0,0).
vec3_invalid- Это используется для недопустимых векторов, например, если результатом функцим станет вектор к точке на пересечении двух параллельных прямых.
Функции пользователя
Длина
vec_t Length()vec_t LengthSqr()Length()returns the vector's length in units. It's faster to useLengthSqr()and square the other value being compared.bool IsLengthGreaterThan(flValue)bool IsLengthLessThan(flValue)- Helpers that perform fast length checks using
LengthSqr(). void Zero()- Sets all elements to 0.
Направление
void Init(vec_t X, Y, Z)- Quickly set an existing vector's ordinates.
void Random(vec_t minVal,vec_t maxVal)- Randomises all three ordinates within the given range.
void Negate()- Reverses the vector's direction without affecting its length.
Vector Max(vOther)Vector Min(vOther)- Clamps the vector's ordinates either above or below the given values. The ordinates won't stay in proportion (i.e. direction might change).
Сравнение
vec_t DistTo(vOther)vec_t DistToSqr(vOther)- Returns the distance between the current vector and
vOtheras a scalar. As ever, the squared flavour is faster. vec_t Dot(vOther)- Returns the dot product of the current vector and
vOther. Vector Cross(vOther)- Returns the cross product of the current vector and
vOther. bool WithinAABox(vecBoxmin,vecBoxmax)- Tests whether the Vector ends within the given box. Box min/max values are local to the Vector.
Приведение
Vector2D AsVector2D()- Casts to Vector2D.
vec_t Length2D()vec_t Length2DSqr()- As their standard equivalents, but ignoring the Z-axis.
Base()- Casts to vec_t*, basically the same as &vec.x or (float*)&vec.
Вспомогательные функции
These globals are all available through cbase.h.
float VectorNormalize(vec)- Divides the vector by its length, normalising it. Modifies the Vector and returns the old length.
vec_t DotProduct(vecA,vecB)- See #Dot product.
void CrossProduct(vecA,vecB,vecResult)- See #Cross product.
void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)- See matrix3x4_t.