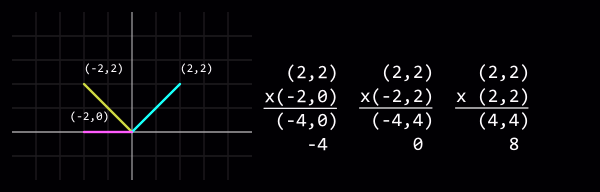Vector: Difference between revisions
m (Reverted edit of RelroDarol, changed back to last version by Solokiller) |
TomEdwards (talk | contribs) (moved from User:TomEdwards/Vector draft) |
||
| Line 1: | Line 1: | ||
{{toc-right}} | |||
{{ | |||
'''Vector''' is a C++ class that represents a line with direction and length, starting at the current [[origin]]. | |||
Each vector contains three <code>[[vec_t]]</code> 'ordinates'. <code>(0,20,5)</code> means 20 [[unit]]s north of and 5 units above the current origin. | |||
{{note|Source's vector class is a 'vector' in the geometric sense of the word, and is ''very'' different to [[Wikipedia:Vector (C++)|the Standard Template Library's]], which is a type of [[Wikipedia:Array|array]]. The STL-style vector has been renamed <code>[[CUtlVector]]</code> in Source.}} | |||
== Declaration == | |||
Vector vecMyVector = Vector(0,20,5); | |||
* The classname <code>Vector</code> is case-sensitive. | |||
* You could also assign to the X, Y and Z member variables separately. | |||
* <code>vec</code> (or sometimes just <code>v</code>) identifies the variable as a <code>Vector</code>. | |||
== Uses == | |||
=== Positioning === | |||
Every entity's position is stored as a vector relative to its [[parent]]. You are likely to be familiar with this idea already as [[coordinates|grid coordinates]]. | |||
The | The parent-relative vector stored by the entity is 'local'; calculating an 'absolute' vector relative to the [[world]] requires extra work. The two Abs functions below do that work for you, but are more [[expensive]]. | ||
* <code>[[GetAbsOrigin()]]</code>, <code>[[SetAbsOrigin()]]</code> | |||
* <code>[[GetLocalOrigin()]]</code>, <code>[[SetLocalOrigin()]]</code> | |||
=== Movement === | |||
An entity attempts to move the length of its velocity vector once per second. The code looks something like this: | |||
= | Vector velocity = Vector(0,5,0); ''// 5 units/second forward'' | ||
Vector vecNewOrigin = GetAbsOrigin() + velocity * [[gpGlobals]]->frametime; ''// frametime is in seconds, e.g. 0.033'' | |||
SetAbsOrigin(vecNewOrigin); | |||
Notice how <code>frametime</code> is used to regulate the entity's speed regardless of how long each frame takes to calculate. See [[#Scalar|scalar multiplication]] for more detail on the operation. | |||
As with the origin, velocity is stored relative to the parent. AbsVelocity represents the velocity relative to the rest frame of the world, and is the more commonly used method. | |||
* <code>[[GetAbsVelocity()]]</code>, <code>[[SetAbsVelocity()]]</code> | |||
* <code>[[GetLocalVelocity()]]</code>, <code>[[SetLocalVelocity()]]</code> | |||
=== Tracelines === | |||
''Main article: [[TraceLines]]'' | |||
Tracing is the process of going from a point A towards another point B, and finding out the first thing that we "hit" on our way from A to B ('''TraceLine'''). | |||
== Operations == | |||
All vectors in an operation must have the same [[origin]] for the result to make sense. Whether a local or absolute origin is used depends on what you're trying to achieve. | |||
=== Addition === | |||
Adding two (or more) vectors '''combines''' them. You have already experienced vector addition if you've ever pushed an object with two hands! | |||
[[Image:Vector_add.png|center|Vector addition: (4,1) + (-3,1) = (1,2)]] | |||
=== Subtraction === | |||
Subtracting one vector from another produces the '''difference''' between the two - in other words, how to get to the first location from the second. The result is local to the ''second'' vector. | |||
[[Image:Vector_subtraction.png|center|Vector subtraction: (2,3) - (-2,1) = (4,2)]] | |||
{{tip|The order in which you subtract defines the direction of the vector.}} | |||
=== Multiplication === | |||
==== Scalar ==== | |||
Multiplying or dividing a vector by a [[Wikipedia:Scalar|scalar]] (i.e. an [[int]] or [[float]]) will change its '''length''' (sometimes called "magnitude") without affecting its direction. | |||
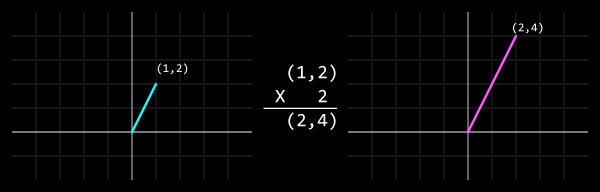
[[Image:Vector-scalar_multiply.png|center|Vector-scalar multiplication: (1,2) x 2 = (2,4)]] | |||
{{tip|Dividing a vector by its length [[normal]]ises it. Use <code>VectorNormalize()</code> to do this quickly.}} | |||
==== Dot product ==== | |||
Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been normalised (see above) is equal to the '''cosine''' of the angle between the two vectors. | |||
One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed. | |||
{{note|''True dot products are only produced when the length of both vectors is 1.'' The [[normal]]isation step has been skipped in the following demonstration to make its equations simpler (but the positive/zero/negative rule still applies).}} | |||
[[Image:Vector_dotproduct.png|center|Vector dot products: (2,2) x (-2,0) = (-4,0) = -4; (2,2) x (-2,2) = (-4,4) = 0; (2,2) x (2,2) = (4,4) = 8]] | |||
This code calculates a dot product with the aid of Source's various helper functions: | |||
Vector vecTarget = GetAbsOrigin() - pTarget->GetAbsOrigin(); ''// Get local vector to target'' | |||
'''VectorNormalize'''(vecTarget); ''// Normalisation needs to be done beforehand'' | |||
Vector vecFacing; | |||
'''[[AngleVectors()|AngleVectors]]'''(GetLocalAngles(),&vecFacing); ''// Convert facing angle to equivalent vector (arrives normalised)'' | |||
float result = '''DotProduct'''(vecTarget,vecFacing); ''// Get the dot product.'' | |||
if (result > 0) | |||
Msg("pTarget is in front of me!\n"); | |||
{{tip|There is no need to normalise if you only care about whether one location is in front of another.}} | |||
==== Cross product ==== | |||
A cross product is a vector '''perpendicular''' to two input vectors. It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis. | |||
The equation is fiddly and doesn't have to be learnt; just use <code>CrossProduct(vecA,vecB,&vecResult)</code>. There generally isn't any need to normalise the input vectors. | |||
== Member functions == | |||
=== Length === | |||
; <code>[[vec_t]] Length()</code> | |||
; <code>vec_t LengthSqr()</code> | |||
: <code>Length()</code> returns the vector's length in [[unit]]s. It's faster to use <code>LengthSqr()</code> and square the value for comparison, however. | |||
; <code>[[bool]] IsLengthGreaterThan(flValue)</code> | |||
; <code>bool IsLengthLessThan(flValue)</code> | |||
: Helpers that perform fast length checks using <code>LengthSqr()</code>. | |||
; <code>void Zero()</code> | |||
: Guess what? | |||
=== Direction === | |||
; <code>void Init(vec_t X, Y, Z)</code> | |||
: Quickly set an existing vector's ordinates. | |||
; <code>void Random(vec_t minVal,vec_t maxVal)</code> | |||
: Randomises all three ordinates within the given range. | |||
; <code>void Negate()</code> | |||
: Reverses the vector's direction without affecting its length. | |||
; <code>Vector Max(vOther)</code> | |||
; <code>Vector Min(vOther)</code> | |||
: Clamps the vector's ordinates either above or below the given values. The ordinates won't stay in proportion (i.e. direction might change). | |||
=== Comparison === | |||
; <code>vec_t DistTo(vOther)</code> | |||
; <code>vec_t DistToSqr(vOther)</code> | |||
: Returns the distance between the current vector and <code>vOther</code> as a scalar. As ever, the squared flavour is faster. | |||
; <code>vec_t Dot(vOther)</code> | |||
: Returns the [[#Dot product|dot product]] of the current vector and <code>vOther</code>. | |||
; <code>Vector Cross(vOther)</code> | |||
: Returns the [[#Cross product|cross product]] of the current vector and <code>vOther</code>. | |||
; <code>bool WithinAABox(vecBoxmin,vecBoxmax)</code> | |||
: Does the vector end within this box? Argument vectors are local. | |||
=== Casts === | |||
; <code>Vector2D AsVector2D()</code> | |||
: Casts to [[Vector2D]]. | |||
; <code>vec_t Length2D()</code> | |||
; <code>vec_t Length2DSqr()</code> | |||
: As their standard equivalents, but ignoring the Z-axis. | |||
; <code>Base()</code> | |||
: Casts to [[vec_t]]. {{todo|What does that achieve?}} | |||
== Helper functions == | |||
; <code>vec_t DotProduct(vecA,vecB)</code> | |||
: See [[#Dot product]]. | |||
; <code>void CrossProduct(const Vector& a, const Vector& b, Vector& result )</code> | |||
: See [[#Cross product]]. | |||
* <code>[[UTIL_VecToYaw()]]</code>, <code>[[UTIL_VecToPitch()]]</code> | |||
* <code>[[AngleVectors()]]</code> and <code>[[VectorAngles()]]</code> | |||
* <code>[[VectorNormalize()]]</code> | |||
== See also == | == See also == | ||
[[Wikipedia: | |||
* [[Wikipedia:Euclidean vector]] | |||
* <code>[[QAngle]]</code> | |||
* <code>[[vec_t]]</code> | |||
* <code>[[VectorVectors]]</code> | |||
* <code>[[CUtlVector]]</code> | |||
[[Category:Glossary]] | |||
[[Category:Variables]] | |||
[[Category:Helpers]] | |||
Revision as of 10:14, 14 April 2009
Vector is a C++ class that represents a line with direction and length, starting at the current origin.
Each vector contains three vec_t 'ordinates'. (0,20,5) means 20 units north of and 5 units above the current origin.
CUtlVector in Source.Declaration
Vector vecMyVector = Vector(0,20,5);
- The classname
Vectoris case-sensitive. - You could also assign to the X, Y and Z member variables separately.
vec(or sometimes justv) identifies the variable as aVector.
Uses
Positioning
Every entity's position is stored as a vector relative to its parent. You are likely to be familiar with this idea already as grid coordinates.
The parent-relative vector stored by the entity is 'local'; calculating an 'absolute' vector relative to the world requires extra work. The two Abs functions below do that work for you, but are more expensive.
Movement
An entity attempts to move the length of its velocity vector once per second. The code looks something like this:
Vector velocity = Vector(0,5,0); // 5 units/second forward Vector vecNewOrigin = GetAbsOrigin() + velocity * gpGlobals->frametime; // frametime is in seconds, e.g. 0.033 SetAbsOrigin(vecNewOrigin);
Notice how frametime is used to regulate the entity's speed regardless of how long each frame takes to calculate. See scalar multiplication for more detail on the operation.
As with the origin, velocity is stored relative to the parent. AbsVelocity represents the velocity relative to the rest frame of the world, and is the more commonly used method.
Tracelines
Main article: TraceLines
Tracing is the process of going from a point A towards another point B, and finding out the first thing that we "hit" on our way from A to B (TraceLine).
Operations
All vectors in an operation must have the same origin for the result to make sense. Whether a local or absolute origin is used depends on what you're trying to achieve.
Addition
Adding two (or more) vectors combines them. You have already experienced vector addition if you've ever pushed an object with two hands!
Subtraction
Subtracting one vector from another produces the difference between the two - in other words, how to get to the first location from the second. The result is local to the second vector.
Multiplication
Scalar
Multiplying or dividing a vector by a scalar (i.e. an int or float) will change its length (sometimes called "magnitude") without affecting its direction.
VectorNormalize() to do this quickly.Dot product
Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been normalised (see above) is equal to the cosine of the angle between the two vectors.
One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed.
This code calculates a dot product with the aid of Source's various helper functions:
Vector vecTarget = GetAbsOrigin() - pTarget->GetAbsOrigin(); // Get local vector to target VectorNormalize(vecTarget); // Normalisation needs to be done beforehand Vector vecFacing; AngleVectors(GetLocalAngles(),&vecFacing); // Convert facing angle to equivalent vector (arrives normalised) float result = DotProduct(vecTarget,vecFacing); // Get the dot product. if (result > 0) Msg("pTarget is in front of me!\n");
Cross product
A cross product is a vector perpendicular to two input vectors. It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis.
The equation is fiddly and doesn't have to be learnt; just use CrossProduct(vecA,vecB,&vecResult). There generally isn't any need to normalise the input vectors.
Member functions
Length
vec_t Length()vec_t LengthSqr()Length()returns the vector's length in units. It's faster to useLengthSqr()and square the value for comparison, however.bool IsLengthGreaterThan(flValue)bool IsLengthLessThan(flValue)- Helpers that perform fast length checks using
LengthSqr(). void Zero()- Guess what?
Direction
void Init(vec_t X, Y, Z)- Quickly set an existing vector's ordinates.
void Random(vec_t minVal,vec_t maxVal)- Randomises all three ordinates within the given range.
void Negate()- Reverses the vector's direction without affecting its length.
Vector Max(vOther)Vector Min(vOther)- Clamps the vector's ordinates either above or below the given values. The ordinates won't stay in proportion (i.e. direction might change).
Comparison
vec_t DistTo(vOther)vec_t DistToSqr(vOther)- Returns the distance between the current vector and
vOtheras a scalar. As ever, the squared flavour is faster. vec_t Dot(vOther)- Returns the dot product of the current vector and
vOther. Vector Cross(vOther)- Returns the cross product of the current vector and
vOther. bool WithinAABox(vecBoxmin,vecBoxmax)- Does the vector end within this box? Argument vectors are local.
Casts
Vector2D AsVector2D()- Casts to Vector2D.
vec_t Length2D()vec_t Length2DSqr()- As their standard equivalents, but ignoring the Z-axis.
Base()- Casts to vec_t. Todo: What does that achieve?
Helper functions
vec_t DotProduct(vecA,vecB)- See #Dot product.
void CrossProduct(const Vector& a, const Vector& b, Vector& result )- See #Cross product.