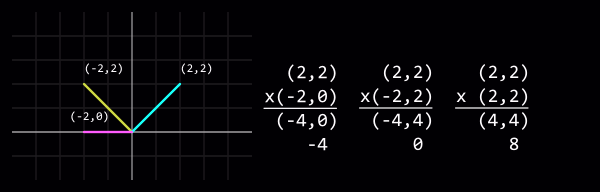Fr/Vector: Difference between revisions
| Line 93: | Line 93: | ||
==== Scalaire ==== | ==== Scalaire ==== | ||
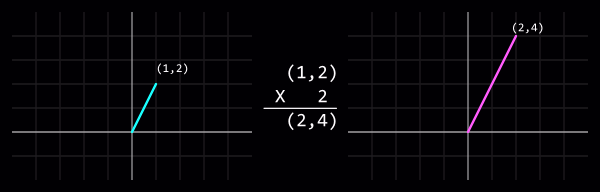
Multiplier ou diviser un vecteur par un [[Wikipedia:Scalar|scalaire]] (nb: un [[int]] ou [[float]]) | Multiplier ou diviser un vecteur par un [[Wikipedia:Scalar|scalaire]] (nb: un [[int]] ou [[float]]) changera ça '''longueur''' (Mathématiquement appellé "magnitude") sans affecter ça direction. | ||
[[Image:Vector-scalar_multiply.png|center|Vector-scalar multiplication: (1,2) x 2 = (2,4)]] | [[Image:Vector-scalar_multiply.png|center|Vector-scalar multiplication: (1,2) x 2 = (2,4)]] | ||
Revision as of 10:14, 15 April 2009
Article en cours de traduction
Vector est une classe C++ représentant une ligne avec une direction et une longueur, elle commence à l'origine (origin) courante. En français cela est tous simplement un vecteur
Chaque vecteur contient trois vec_t 'ordonées' (ordinates). (0,20,5) signifie 20 unités en face et 5 unités au dessus de l'origin courante.
CUtlVector dans Source.Déclaration
Vector vecMyVector = Vector(0,20,5);
- Le nom de classe (classname)
Vectorest sensible à la case. - Vous pouvez aussi assigner les variables X, Y et Z séparément.
vec(ou simplementv) comme suffix, identifie une variable comme étend un vecteurVector.
Orientation
Dans la majorité des cas, les vecteurs sont considérés comme étends orientés de manière 'relative' au coordonnées global. Ainsi, ils sont alignés sur les axes du monde 3D(world-axis-aligned): l'horizon ou composante X, est aligné d'est en ouest. La profondeur de champs ou composante Y, est aligné du nord au sud. L'altitude ou composante Z, est aligné de haut en bas.
Cependant dans quelques cas, le vecteur peut aussi être considéré comme étend aligné sur les axes d'un objet (object-axis-aligned) - orienté dans le sens des coordonées et angles locaux de son parent. C'est dans ce cas que certaines fonctions sont utilisées pour appliquer une force à un objet physique. Ainsi les codeurs doivent en être conscient, et vérifier tout commentaires spécifiés quand ils sont dans le doute.
Un exemple de cela serait dans le fichier vphysics_interface.cpp pour la classe IPhysicsObject :
// force the velocity to a new value
// NOTE: velocity is in worldspace, angularVelocity is relative to the object's
// local axes (just like pev->velocity, pev->avelocity)
virtual void SetVelocity( const Vector *velocity, const AngularImpulse *angularVelocity ) = 0;
Pour attribuer une force world-axis-aligned (cf plus haut) à une force object-axis-aligned, vous pouvez utiliser :
VectorIRotate( aiIn, EntityToWorldTransform(), aiOut );
Utilisation
Positionnement
Toutes les positions des entités sont stockées comme des vecteurs relatif à leurs parent. Vous devez être familiarisé avec cette notion via le système de la grille de coordonées cartésiennes.
Les vecteurs relatifs à un parent (apparentés) stockés par l'entité sont 'locaux'; Calculer une un vecteur 'absolue' relatif au monde 3D requiert un peu plus de calcule. Les deux fonctions Abs ci-dessous les font pour vous, mais sont plus gourmande en ressources.
Mouvement
An entity attempts to move the length of its velocity vector once per second. The code looks something like this:
Vector velocity = Vector(0,5,0); // 5 units/second in the +Y direction Vector vecNewOrigin = GetAbsOrigin() + velocity * gpGlobals->frametime; // frametime is in seconds, e.g. 0.033 SetAbsOrigin(vecNewOrigin);
Notice how frametime is used to regulate the entity's speed regardless of how long each frame takes to calculate. See scalar multiplication for more detail on the operation.
As with the origin, velocity is stored relative to the parent. AbsVelocity represents the velocity relative to the rest frame of the world, and is the more commonly used method.
Tracelines
Article principal: TraceLines
Tracing is the process of going from a point A towards another point B, and finding out the first thing that we "hit" on our way from A to B (TraceLine).
Opérations
All vectors in an operation must have the same origin for the result to make sense. Whether a local or absolute origin is used depends on what you're trying to achieve.
Addition
Adding two (or more) vectors combines them. You have already experienced vector addition if you've ever pushed an object with two hands!
Soustraction
Subtracting one vector from another produces the difference between the two - in other words, how to get to the first location from the second. The result is local to the second vector.
Multiplication
Scalaire
Multiplier ou diviser un vecteur par un scalaire (nb: un int ou float) changera ça longueur (Mathématiquement appellé "magnitude") sans affecter ça direction.
VectorNormalize() to do this quickly.Produit scalaire (dot product)
Multiplier deux vecteurs normalisés puis additionné leurs ordonnés obtenues est appellé Produit Scalaire (dot product en anglais), cela permet de savoir l'angle qui sépare les deux vecteurs (Mathématiquement appelé l'argument des vecteurs). Pourquoi dire Argument au lieu d'Angle tout simplement car la valeurs obtenue est un cosinus et non pas une valeur en degrée. Si celle-ci vaut +1 alors les vecteurs sont alignés, si elle vaut 0 alors les vecteurs sont perpendiculaire l'un à l'autre, si elle vaut -1 alors les vecteurs sont opposés
Ce code calcule un produit scalaire avec les diverses fontions d'aide de Source.
Vector vecTarget = GetAbsOrigin() - pTarget->GetAbsOrigin(); // Get local vector to target
VectorNormalize(vecTarget); // Normalisation needs to be done beforehand
Vector vecFacing;
AngleVectors(GetLocalAngles(),&vecFacing); // Convert facing angle to equivalent vector (arrives normalised)
float result = DotProduct(vecTarget,vecFacing); // Get the dot product.
if (result > 0)
Msg("pLa cible est devant moi!\n");
Le produit vectoriel (cross product)
Le produit vectoriel ou cross product en anglais, est le vecteur perpendiculaire à deux autres vecteurs. Il est utilisé pour extrapoler uen troisièem dimension à partir de deux vecteurs: Le produit vectoriel d'un vecteur pointant le bas de l'axe X et d'un vecteur pointant le bas de l'axe Y, sera un vecteur pointant le bas de l'axe Z.
Si l'équation suivante est trop compliquée ne vous en faite pas, Source à des fonctions qui font ça pour vous! Soit un vecteur A et un vecteur B, ordonné en X, Y et Z. On obtient leur produit vectoriel dans un vecteur N comme suis:
N.x = (A.y * B.z) - (A.z * B.y)
N.y = (A.z * B.x) - (A.x * B.z)
N.z = (A.x * B.y) - (A.y * B.x)
Dans source il suffit de faire CrossProduct(vecA,vecB,&vecResult).
Il n'est en général pas nécessaire de normaliser les vecteurs passés en argument. Il est rare que les moddeurs utilisent le produit vectoriel, comme toujours, si cela est requit, soyez conscient du niveau de mathématique requit pour comprendre ce genre d'opération.
Fonctions membres
Longueur
vec_t Length()vec_t LengthSqr()Length()retourne la longueur du vecteur en unités. Cepdendant il est plus rapide d'utiliserLengthSqr()et de prendre la racine du résultat pour comparer .bool IsLengthGreaterThan(flValue)bool IsLengthLessThan(flValue)- Effectuer un rapide test de longueur grâce à la focntion d'aide
LengthSqr(). void Zero()- Ce qui veux dire?
Direction
void Init(vec_t X, Y, Z)- Définit rapidement l'ordonée d'un vecteur existant.
void Random(vec_t minVal,vec_t maxVal)- Attribue des valeurs aléatoire pour les trois ordonnées dans l'interval donné.
void Negate()- Inverse la direction du vecteur sans en affecter la longueur.
Vector Max(vOther)Vector Min(vOther)- "Pince" les ordonées du vecteur qu'elles soit au-dessus ou au-dessous des valeurs données. Les ordonnées ne resteront pas proportionnels (nb: La direction peu changer)
Comparaison
vec_t DistTo(vOther)vec_t DistToSqr(vOther)- Retourne la distance entre le vecteur courant et de
vOthercomme un scalaire. Comme toujours, une racine (flavour?) est plus rapide. vec_t Dot(vOther)- Retourne le produit scalaire du vecteur courant et de
vOther. Vector Cross(vOther)- Retourne le produit vectoriel du vecteur courant et de
vOther. bool WithinAABox(vecBoxmin,vecBoxmax)- Est-ce que le vecteur finit avec cetet boite? L'Argument du vecteur est local.
Casts
Vector2D AsVector2D()- Cast en Vector2D.
vec_t Length2D()vec_t Length2DSqr()- Cast dans leurs équivalent standard, en ignorant l'axe Z.
Base()- Cast en vec_t. À Faire: Quand résult-il?
Fonctions d'aide
Elles sont disponibles dans le fichier cbase.h.
vec_t DotProduct(vecA,vecB)- Voir produit scalaire.
void CrossProduct(vecA,vecB,vecResult)- Voir produit vectoriel.
void VectorRotate(in1,in2,out)void VectorIRotate(in1,in2,out)- Transforme un vecteur. Plusieurs surcharge accepte un vector ou un float pour le paramètre
in1et unmatrix3x4_t,QAngleouQuaternionpour le paramètrein2.