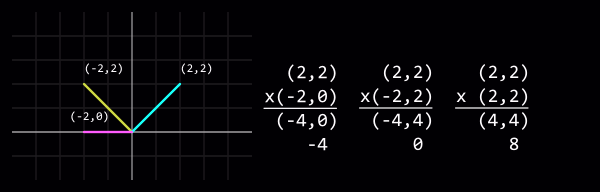Vector: Difference between revisions
m (→Movement) |
(Rewrite Template:Lang to Template:LanguageBar. This action was performed by a bot.) |
||
| (36 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
{{LanguageBar|Vector}} | |||
{{toc-right}} | {{toc-right}} | ||
'''Vector''' is a C++ class that represents a line with direction and length, starting at the current [[origin]]. | '''<code>Vector</code>''' is a C++ class that represents a line with direction and length, starting at the current [[origin]]. | ||
== Ordinates == | |||
Each vector contains three <code>[[vec_t]]</code> ordinates. | |||
;X | |||
:+forward/-backward | |||
;Y | |||
:+left/-right | |||
;Z | |||
:+up/-down | |||
<code>(1,20,5)</code> means 1 [[unit]] forward, 20 units to the left and 5 units above the current origin. | |||
{{note|Source's vector class is geometric and ''very'' different from [[Wikipedia:Vector (C++)|the Standard Template Library's]], which is a type of [[Wikipedia:Array|array]]. The STL-style vector has been renamed <code>[[CUtlVector]]</code> in Source.}} | {{note|[[Source]]'s vector class{{clarify}} is geometric and ''very'' different from [[Wikipedia:Vector (C++)|the Standard Template Library's]], which is a type of [[Wikipedia:Array|array]]. The STL-style vector has been renamed <code>[[CUtlVector]]</code> in Source.}} | ||
== Declaration == | == Declaration == | ||
{{pre|1=Vector vecMyVector = Vector(1,20,5);}} | |||
* The classname <code>Vector</code> is case-sensitive. | * The classname <code>Vector</code> is case-sensitive. | ||
* You | * You can construct it by defining the X, Y and Z member variables separately, pass a single value for all three or copying the data of another Vector. | ||
* <code>vec</code> (or sometimes just <code>v</code>) identifies the variable as a | * The prefix <code>vec</code> (or sometimes just <code>v</code>) identifies the variable as a vector. | ||
== Orientation == | |||
A vector does not have an orientation; that is determined by the code that uses it. | |||
In the vast majority of cases a vector will be interpreted as '''world axis aligned''' regardless of an entity's rotation, but there are few cases (e.g. applying physics forces), where they are considered '''object axis aligned'''. | |||
< | There is no way of telling which interpretation will be used from the variable, so check for function comments when in doubt. Use [[#Helper functions|<code>VectorRotate()</code>]] and [[#Helper functions|<code>VectorIRotate()</code>]] to translate between alignments. | ||
== Uses == | == Uses == | ||
; Positioning | |||
: Every entity's position ('origin') is stored as a vector relative to its [[parent]]: you are likely to be familiar with this idea already as [[coordinates|Cartesian grid coordinates]]. See <code>[[GetAbsOrigin()]]</code> for more details. | |||
Every entity's position is stored as a vector relative to its [[parent]] | ; Movement | ||
: An entity attempts to move the length of its [[velocity]] vector once per second. | |||
; Collision Traces | |||
: A [[UTIL TraceLine|Traceline]] or [[UTIL TraceHull|-hull]] is fired from one point to another, detecting what it "hits" along its path. | |||
An entity attempts to move the length of its velocity vector once per second. | |||
== Operations == | == Operations == | ||
| Line 73: | Line 51: | ||
Adding two (or more) vectors '''combines''' them. You have already experienced vector addition if you've ever pushed an object with two hands! | Adding two (or more) vectors '''combines''' them. You have already experienced vector addition if you've ever pushed an object with two hands! | ||
[[ | [[File:Vector_add.png|center|Vector addition: (4,1) + (-3,1) = (1,2)]] | ||
=== Subtraction === | === Subtraction === | ||
| Line 79: | Line 57: | ||
Subtracting one vector from another produces the '''difference''' between the two - in other words, how to get to the first location from the second. The result is local to the ''second'' vector. | Subtracting one vector from another produces the '''difference''' between the two - in other words, how to get to the first location from the second. The result is local to the ''second'' vector. | ||
[[ | [[File:Vector_subtraction.png|center|Vector subtraction: (2,3) - (-2,1) = (4,2)]] | ||
{{tip|The order in which you subtract defines the direction of the vector.}} | {{tip|The order in which you subtract defines the direction of the vector.}} | ||
| Line 89: | Line 67: | ||
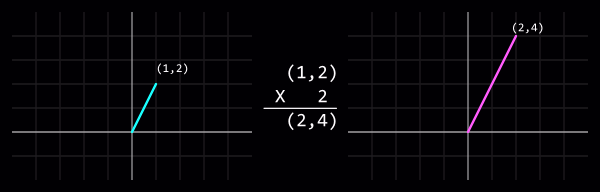
Multiplying or dividing a vector by a [[Wikipedia:Scalar|scalar]] (i.e. an [[int]] or [[float]]) will change its '''length''' (sometimes called "magnitude") without affecting its direction. | Multiplying or dividing a vector by a [[Wikipedia:Scalar|scalar]] (i.e. an [[int]] or [[float]]) will change its '''length''' (sometimes called "magnitude") without affecting its direction. | ||
[[ | [[File:Vector-scalar_multiply.png|center|Vector-scalar multiplication: (1,2) x 2 = (2,4)]] | ||
{{tip|Dividing a vector by its length [[normal]]ises it. Use <code>VectorNormalize()</code> to do this quickly.}} | {{tip|Dividing a vector by its length [[normal]]ises it. Use <code>VectorNormalize()</code> to do this quickly.}} | ||
| Line 95: | Line 73: | ||
==== Dot product ==== | ==== Dot product ==== | ||
Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been | Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been [[normal]]ised is equal to the '''cosine''' of the angle between the two vectors. | ||
One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed. | One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed. | ||
| Line 101: | Line 79: | ||
{{note|''True dot products are only produced when the length of both vectors is 1.'' The [[normal]]isation step has been skipped in the following demonstration to make its equations simpler (but the positive/zero/negative rule still applies).}} | {{note|''True dot products are only produced when the length of both vectors is 1.'' The [[normal]]isation step has been skipped in the following demonstration to make its equations simpler (but the positive/zero/negative rule still applies).}} | ||
[[ | [[File:Vector_dotproduct.png|center|Vector dot products: (2,2) x (-2,0) = (-4,0) = -4; (2,2) x (-2,2) = (-4,4) = 0; (2,2) x (2,2) = (4,4) = 8]] | ||
This code calculates a dot product with the aid of Source's various helper functions: | This code calculates a dot product with the aid of Source's various helper functions: | ||
<source lang=cpp style="display:table-cell; background:transparent"> | |||
Vector vecTarget = pTarget->GetAbsOrigin() - GetAbsOrigin(); // Get local vector to target | |||
VectorNormalize(vecTarget); // Normalisation needs to be done beforehand | |||
Vector vecFacing; | |||
AngleVectors(GetLocalAngles(),&vecFacing); // Convert facing angle to equivalent vector (arrives normalised) | |||
float dot = DotProduct(vecTarget,vecFacing); // Get the dot product | |||
if (dot > 0) | |||
Msg("pTarget is in front of me!\n"); | |||
</source> | |||
{{tip|There is no need to normalise if you only care about whether one location is in front of another.}} | {{tip|There is no need to normalise if you only care about whether one location is in front of another.}} | ||
In this code, the expression {{code|dot > 0}} is true if the angle between the input vectors is < 90°. If you need two vectors to be < x degrees apart, then {{code|dot > cos(x°)}} must be true, where cos(x°) is a constant. Note that this way, the dot product allows to check the angle between two vectors without calling the rather expensive cosine function at runtime. | |||
{{important|1=There are various entities with keyvalues denoting a maximum angle as a float in the range -1.0 to 1.0, for example the <tt>FieldOfView</tt> keyvalue of {{ent|trigger_look}}. Such a keyvalue commonly refers to a dot product, which means that it is <b style=white-space:nowrap>not a linear</b> function of the desired angle. A common mistake would be to set it to a value of 0.5 which is intended to correspond to an angle of 45°, but instead, the correct value would be cos(45°) ≈ 0.707!}} | |||
{| class=wikitable | |||
!style=background:#333| Angle between input vectors | |||
| x° || cos<sup>-1</sup>(<tt>dot</tt>) || 0° || 1° || 2° || 5° || 10° || 15° || 30° || 45° || 60° || 75° || 90° || 120° || 180° | |||
|- | |||
!style=background:#333| Dot of normalized input vectors | |||
| cos(x°) || <tt>dot</tt> || 1.0 || 0.99985 || 0.99939 || 0.99619 || 0.98481 || 0.96593 || 0.86603 || 0.70711 || 0.5 || 0.25882 || 0 || -0.5 || -1.0 | |||
|} | |||
==== Cross product ==== | ==== Cross product ==== | ||
A cross product is a vector '''perpendicular''' to two input vectors. | A [[w:cross product|cross product]] is a vector '''perpendicular''' to two input vectors. Its direction can be determined with the [[w:right-hand rule|right-hand rule]]. Its length is equal to the area of the parallelogram that the vectors span. If the input vectors point in the same direction or if one of them is the zero vector, then their cross product is the zero vector. | ||
The equation is fiddly and doesn't have to be learnt; just use <code>CrossProduct(vecA,vecB,&vecResult)</code>. There generally isn't any need to normalise the input vectors. Most modders will likely only use cross products rarely, if ever - but if required, be aware that a [http://mathworld.wolfram.com/CrossProduct.html moderate amount of math] is required to [ | It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis. | ||
The equation is fiddly and doesn't have to be learnt; just use <code>CrossProduct(vecA,vecB,&vecResult)</code>. There generally isn't any need to normalise the input vectors. Most modders will likely only use cross products rarely, if ever - but if required, be aware that a [http://mathworld.wolfram.com/CrossProduct.html moderate amount of math] is required to properly understand this operation. | |||
== Rotation == | |||
Rotating a Vector requires a [[matrix3x4 t|matrix]], so can't be done with an operation like those above. Thankfully you don't need to get involved in the gritty details: just call <code>VectorRotate(Vector in, QAngle in, Vector& out)</code>. | |||
== Special Vectors == | |||
Source defines two special Vectors: | |||
; <code>vec3_origin</code> | |||
: Vector(0,0,0). | |||
; <code>vec3_invalid</code> | |||
: This is used for invalid Vectors, e.g. if you need to return a Vector in a function, but something is not possible (such as the intersection-point of two parallel straight lines). | |||
== Member functions == | == Member functions == | ||
| Line 129: | Line 136: | ||
; <code>[[vec_t]] Length()</code> | ; <code>[[vec_t]] Length()</code> | ||
; <code>vec_t LengthSqr()</code> | ; <code>vec_t LengthSqr()</code> | ||
: <code>Length()</code> returns the vector's length in [[unit]]s. It's faster to use <code>LengthSqr()</code> and square the value | : <code>Length()</code> returns the vector's length in [[unit]]s. It's faster to use <code>LengthSqr()</code> and square the other value being compared. | ||
; <code>[[bool]] IsLengthGreaterThan(flValue)</code> | ; <code>[[bool]] IsLengthGreaterThan(flValue)</code> | ||
; <code>bool IsLengthLessThan(flValue)</code> | ; <code>bool IsLengthLessThan(flValue)</code> | ||
: Helpers that perform fast length checks using <code>LengthSqr()</code>. | : Helpers that perform fast length checks using <code>LengthSqr()</code>. | ||
; <code>void Zero()</code> | ; <code>void Zero()</code> | ||
: | : Sets all elements to 0. | ||
=== Direction === | === Direction === | ||
| Line 158: | Line 165: | ||
: Returns the [[#Cross product|cross product]] of the current vector and <code>vOther</code>. | : Returns the [[#Cross product|cross product]] of the current vector and <code>vOther</code>. | ||
; <code>bool WithinAABox(vecBoxmin,vecBoxmax)</code> | ; <code>bool WithinAABox(vecBoxmin,vecBoxmax)</code> | ||
: | : Tests whether the Vector ends within the given box. Box min/max values are local to the Vector. | ||
=== Casts === | === Casts === | ||
| Line 168: | Line 175: | ||
: As their standard equivalents, but ignoring the Z-axis. | : As their standard equivalents, but ignoring the Z-axis. | ||
; <code>Base()</code> | ; <code>Base()</code> | ||
: Casts to [[ | : Casts to [[vec t]]*, basically the same as &vec.x or (float*)&vec. | ||
== Helper functions == | == Helper functions == | ||
; <code>vec_t DotProduct(vecA,vecB)</code> | These globals are all available through <code>cbase.h</code>. | ||
; <code>[[float]] VectorNormalize(vec)</code> | |||
: Divides the vector by its length, [[normal]]ising it. Modifies the Vector and returns the old length. | |||
; <code>[[vec_t]] DotProduct(vecA,vecB)</code> | |||
: See [[#Dot product]]. | : See [[#Dot product]]. | ||
; <code>void CrossProduct( | ; <code>void CrossProduct(vecA,vecB,vecResult)</code> | ||
: See [[#Cross product]]. | : See [[#Cross product]]. | ||
; <code>void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)</code> | |||
* <code> | : See [[matrix3x4 t]]. | ||
* | * [[UTIL VecToYaw()|<code>UTIL_VecToYaw()</code> / <code>UTIL_VecToPitch()</code>]] | ||
* [[AngleVectors()|<code>AngleVectors()</code> / <code>VectorAngles()</code>]] | |||
== See also == | == See also == | ||
* [[Coordinates]] | |||
* [[Wikipedia:Euclidean vector]] | * [[Wikipedia:Euclidean vector]] | ||
* <code>[[vec_t]]</code> | * <code>[[vec_t]]</code> | ||
* <code>[[Vector2D]]</code> | * <code>[[Vector2D]]</code> | ||
* <code>[[QAngle]]</code> | * <code>[[QAngle]]</code> | ||
* <code>[[matrix3x4_t]]</code> | |||
* <code>[[CUtlVector]]</code> | * <code>[[CUtlVector]]</code> | ||
[[Category:Source class]] | |||
[[Category:Helpers]] | |||
[[Category:Glossary]] | [[Category:Glossary]] | ||
[[Category:Variables]] | [[Category:Variables]] | ||
[[Category:Helpers]] | [[Category:Helpers]] | ||
Latest revision as of 17:41, 18 July 2025
Vector is a C++ class that represents a line with direction and length, starting at the current origin.
Ordinates
Each vector contains three vec_t ordinates.
- X
- +forward/-backward
- Y
- +left/-right
- Z
- +up/-down
(1,20,5) means 1 unit forward, 20 units to the left and 5 units above the current origin.
CUtlVector in Source.Declaration
Vector vecMyVector = Vector(1,20,5);
- The classname
Vectoris case-sensitive. - You can construct it by defining the X, Y and Z member variables separately, pass a single value for all three or copying the data of another Vector.
- The prefix
vec(or sometimes justv) identifies the variable as a vector.
Orientation
A vector does not have an orientation; that is determined by the code that uses it.
In the vast majority of cases a vector will be interpreted as world axis aligned regardless of an entity's rotation, but there are few cases (e.g. applying physics forces), where they are considered object axis aligned.
There is no way of telling which interpretation will be used from the variable, so check for function comments when in doubt. Use VectorRotate() and VectorIRotate() to translate between alignments.
Uses
- Positioning
- Every entity's position ('origin') is stored as a vector relative to its parent: you are likely to be familiar with this idea already as Cartesian grid coordinates. See
GetAbsOrigin()for more details. - Movement
- An entity attempts to move the length of its velocity vector once per second.
- Collision Traces
- A Traceline or -hull is fired from one point to another, detecting what it "hits" along its path.
Operations
All vectors in an operation must have the same origin for the result to make sense. Whether a local or absolute origin is used depends on what you're trying to achieve.
Addition
Adding two (or more) vectors combines them. You have already experienced vector addition if you've ever pushed an object with two hands!
Subtraction
Subtracting one vector from another produces the difference between the two - in other words, how to get to the first location from the second. The result is local to the second vector.
Multiplication
Scalar
Multiplying or dividing a vector by a scalar (i.e. an int or float) will change its length (sometimes called "magnitude") without affecting its direction.
VectorNormalize() to do this quickly.Dot product
Multiplying two vectors then adding the result's ordinates produces a dot product, which when both vectors have been normalised is equal to the cosine of the angle between the two vectors.
One use of a dot product is to tell how closely the two vectors align. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed.
This code calculates a dot product with the aid of Source's various helper functions:
Vector vecTarget = pTarget->GetAbsOrigin() - GetAbsOrigin(); // Get local vector to target
VectorNormalize(vecTarget); // Normalisation needs to be done beforehand
Vector vecFacing;
AngleVectors(GetLocalAngles(),&vecFacing); // Convert facing angle to equivalent vector (arrives normalised)
float dot = DotProduct(vecTarget,vecFacing); // Get the dot product
if (dot > 0)
Msg("pTarget is in front of me!\n");
In this code, the expression dot > 0 is true if the angle between the input vectors is < 90°. If you need two vectors to be < x degrees apart, then dot > cos(x°) must be true, where cos(x°) is a constant. Note that this way, the dot product allows to check the angle between two vectors without calling the rather expensive cosine function at runtime.
| Angle between input vectors | x° | cos-1(dot) | 0° | 1° | 2° | 5° | 10° | 15° | 30° | 45° | 60° | 75° | 90° | 120° | 180° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dot of normalized input vectors | cos(x°) | dot | 1.0 | 0.99985 | 0.99939 | 0.99619 | 0.98481 | 0.96593 | 0.86603 | 0.70711 | 0.5 | 0.25882 | 0 | -0.5 | -1.0 |
Cross product
A cross product is a vector perpendicular to two input vectors. Its direction can be determined with the right-hand rule. Its length is equal to the area of the parallelogram that the vectors span. If the input vectors point in the same direction or if one of them is the zero vector, then their cross product is the zero vector.
It's used to extrapolate a third dimension from just two: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis.
The equation is fiddly and doesn't have to be learnt; just use CrossProduct(vecA,vecB,&vecResult). There generally isn't any need to normalise the input vectors. Most modders will likely only use cross products rarely, if ever - but if required, be aware that a moderate amount of math is required to properly understand this operation.
Rotation
Rotating a Vector requires a matrix, so can't be done with an operation like those above. Thankfully you don't need to get involved in the gritty details: just call VectorRotate(Vector in, QAngle in, Vector& out).
Special Vectors
Source defines two special Vectors:
vec3_origin- Vector(0,0,0).
vec3_invalid- This is used for invalid Vectors, e.g. if you need to return a Vector in a function, but something is not possible (such as the intersection-point of two parallel straight lines).
Member functions
Length
vec_t Length()vec_t LengthSqr()Length()returns the vector's length in units. It's faster to useLengthSqr()and square the other value being compared.bool IsLengthGreaterThan(flValue)bool IsLengthLessThan(flValue)- Helpers that perform fast length checks using
LengthSqr(). void Zero()- Sets all elements to 0.
Direction
void Init(vec_t X, Y, Z)- Quickly set an existing vector's ordinates.
void Random(vec_t minVal,vec_t maxVal)- Randomises all three ordinates within the given range.
void Negate()- Reverses the vector's direction without affecting its length.
Vector Max(vOther)Vector Min(vOther)- Clamps the vector's ordinates either above or below the given values. The ordinates won't stay in proportion (i.e. direction might change).
Comparison
vec_t DistTo(vOther)vec_t DistToSqr(vOther)- Returns the distance between the current vector and
vOtheras a scalar. As ever, the squared flavour is faster. vec_t Dot(vOther)- Returns the dot product of the current vector and
vOther. Vector Cross(vOther)- Returns the cross product of the current vector and
vOther. bool WithinAABox(vecBoxmin,vecBoxmax)- Tests whether the Vector ends within the given box. Box min/max values are local to the Vector.
Casts
Vector2D AsVector2D()- Casts to Vector2D.
vec_t Length2D()vec_t Length2DSqr()- As their standard equivalents, but ignoring the Z-axis.
Base()- Casts to vec t*, basically the same as &vec.x or (float*)&vec.
Helper functions
These globals are all available through cbase.h.
float VectorNormalize(vec)- Divides the vector by its length, normalising it. Modifies the Vector and returns the old length.
vec_t DotProduct(vecA,vecB)- See #Dot product.
void CrossProduct(vecA,vecB,vecResult)- See #Cross product.
void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)- See matrix3x4 t.