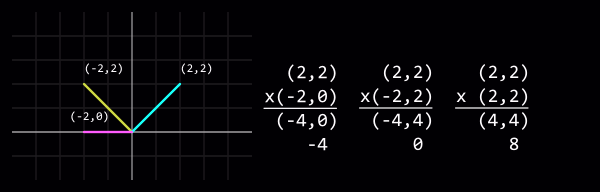De/Vector: Difference between revisions
m (obsolete language category) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
{{toc-right}} | {{toc-right}} | ||
'''<code>Vector</code>''' ist eine C++-Klasse, die eine Linie mit einer Richtung und einer Länge repräsentiert, die beim aktuellen | '''<code>Vector</code>''' ist eine C++-Klasse, die eine Linie mit einer Richtung und einer Länge repräsentiert, die beim aktuellen {{L|Origin|Ursprung}} beginnt. Jeder Vektor beinhaltet 3 <code>{{L|vec_t}}</code> Koordinaten: | ||
* '''X''' +vorwärts/-rückwärts | * '''X''' +vorwärts/-rückwärts | ||
| Line 9: | Line 9: | ||
* '''Z''' +oben/-unten | * '''Z''' +oben/-unten | ||
<code>(1,20,5)</code> bedeutet 1 | <code>(1,20,5)</code> bedeutet 1 {{L|unit|Einheit}} vorwärts, 20 Einheiten nach links und 5 Einheiten über dem aktuellen Ursprung. | ||
{{Note|Sources Vektorklasse ist geometrisch und unterscheidet sich ''sehr'' von der | {{Note|Sources Vektorklasse ist geometrisch und unterscheidet sich ''sehr'' von der {{L|Wikipedia:Vector (C++)|Standard-Tamplate-Bibliothek}}, was eine Art von {{L|Wikipedia:Array|Array}} ist. der STL-Vektor wurde in <code>{{L|CUtlVector}}</code> in Source umbenannt.}} | ||
== Deklaration == | == Deklaration == | ||
| Line 32: | Line 32: | ||
; Positionierung | ; Positionierung | ||
: Jede Position einer Entity ('Ursprung' - "'origin'") wird als Vektor relativ zu seinem | : Jede Position einer Entity ('Ursprung' - "'origin'") wird als Vektor relativ zu seinem {{L|parent|übergeordneten Element}}: wahrscheinlich sind diese bereits als {{L|coordinates|kartesische Koordinaten}} bekannt. Siehe <code>{{L|GetAbsOrigin()}}</code> für mehr Details. | ||
; Bewegung | ; Bewegung | ||
: Eine Entity versucht, sich je Sekunde um die Länge seiner | : Eine Entity versucht, sich je Sekunde um die Länge seiner {{L|velocity|Geschwindigkeit}} zu bewegen. | ||
; Kollisionsspuren | ; Kollisionsspuren | ||
: Eine | : Eine {{L|UTIL_TraceLine|Traceline}} oder {{L|UTIL_TraceHull|TraceHull}} wird von einem Punkt auf einen anderen gefeuert, um aufzuspüren, was es auf seinem Weg trifft. | ||
== Operationen == | == Operationen == | ||
Alle Vektoren müssen innerhalb einer Operation den gleichen | Alle Vektoren müssen innerhalb einer Operation den gleichen {{L|origin|Ursprung}} haben, damit das Ergebnis Sinn ergibt. Ob eine lokaler oder absoluter Ursprung verwendet wird, hängt davon ab, was erreicht werden soll. | ||
=== Addition === | === Addition === | ||
| Line 59: | Line 59: | ||
==== Skalar ==== | ==== Skalar ==== | ||
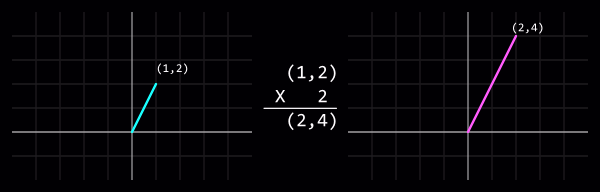
einen Vektor mit einem | einen Vektor mit einem {{L|Wikipedia:Scalar|Skalar}} (z. B. ein {{L|int}} oder {{L|float}}) zu multiplizieren oder zu dividieren wird dessen '''Länge''' (gelegentlich "Größe" - "magnitude" - genannt), ohne die Richtung zu beeinflussen. | ||
[[File:Vector-scalar_multiply.png|center|Vector-Skalar-Multiplikation: (1,2) x 2 = (2,4)]] | [[File:Vector-scalar_multiply.png|center|Vector-Skalar-Multiplikation: (1,2) x 2 = (2,4)]] | ||
{{Tip|Einen Vektor durch seine Länge zu teilen, | {{Tip|Einen Vektor durch seine Länge zu teilen, {{L|normal|normalisiert}} ihn. Man kann <code>VectorNormalize()</code> verwenden, um dies schnell zu erledigen.}} | ||
==== Skalarprodukt ==== | ==== Skalarprodukt ==== | ||
Das Multiplizieren zweier Vektoren und addieren der Komponenten des resultierenden Vektors erzeugt ein Skalarprodukt, welches dem '''Cosinus''' des Winkels zwischen den Vektoren entspricht, wenn beide Vektoren | Das Multiplizieren zweier Vektoren und addieren der Komponenten des resultierenden Vektors erzeugt ein Skalarprodukt, welches dem '''Cosinus''' des Winkels zwischen den Vektoren entspricht, wenn beide Vektoren {{L|normal|normalisiert}}. | ||
Eine Verwendung von Skalarprodukten ist, zu sagen, wie dicht die beiden Vektoren verlaufen. +1 bedeutet, sie stimmen überein, 0 bedeutet, sie stehen senkrecht zueinander und -1 bedeutet, sie sind entgegengesetzt. | Eine Verwendung von Skalarprodukten ist, zu sagen, wie dicht die beiden Vektoren verlaufen. +1 bedeutet, sie stimmen überein, 0 bedeutet, sie stehen senkrecht zueinander und -1 bedeutet, sie sind entgegengesetzt. | ||
{{Note|''Echte Skalarprodukte entstehen nur, wenn die Länge beider Vektoren 1 ist.'' Der | {{Note|''Echte Skalarprodukte entstehen nur, wenn die Länge beider Vektoren 1 ist.'' Der {{L|normal|Normalisation}}sschritt wurde im folgenden Beispiel ausgelassen, um die Gleichungen einfacher zu machen (die Positiv/Null/Negativ-Regel gilt dennoch).}} | ||
[[File:Vector_dotproduct.png|center|Vector-Skalarprodukt: (2,2) x (-2,0) = (-4,0) = -4; (2,2) x (-2,2) = (-4,4) = 0; (2,2) x (2,2) = (4,4) = 8]] | [[File:Vector_dotproduct.png|center|Vector-Skalarprodukt: (2,2) x (-2,0) = (-4,0) = -4; (2,2) x (-2,2) = (-4,4) = 0; (2,2) x (2,2) = (4,4) = 8]] | ||
| Line 96: | Line 96: | ||
Ein Kreuzprodukt ist ein Vektor, der '''senkrecht''' zu 2 Eingangsvektoren steht. Er wird verwendet die 3. Dimenson aus nur 2 zu extrapolieren: das Kreuzprodukt eines Vektors, der die X-Achse entlang zeigt und eines Vektors, der die Y-Achse entlang zeigt, ist ein Vektor, der die Z-Achse entlang zeigt. | Ein Kreuzprodukt ist ein Vektor, der '''senkrecht''' zu 2 Eingangsvektoren steht. Er wird verwendet die 3. Dimenson aus nur 2 zu extrapolieren: das Kreuzprodukt eines Vektors, der die X-Achse entlang zeigt und eines Vektors, der die Y-Achse entlang zeigt, ist ein Vektor, der die Z-Achse entlang zeigt. | ||
Die Gleichung ist knifflig und muss nicht gelernt werden; man kann <code>CrossProduct(vecA,vecB,&vecResult)</code> verwenden. Es besteht grundsätzlich keine Notwendigkeit, die Eingabevektoren zu normalisieren. Die meisten Modder werden Kreuzprodukte nur selten verwenden, wenn überhaupt. Wenn jedoch benötigt, dass eine [http://mathworld.wolfram.com/CrossProduct.html mäßige Menge Mathematik] benötigt wird, um diese Operation | Die Gleichung ist knifflig und muss nicht gelernt werden; man kann <code>CrossProduct(vecA,vecB,&vecResult)</code> verwenden. Es besteht grundsätzlich keine Notwendigkeit, die Eingabevektoren zu normalisieren. Die meisten Modder werden Kreuzprodukte nur selten verwenden, wenn überhaupt. Wenn jedoch benötigt, dass eine [http://mathworld.wolfram.com/CrossProduct.html mäßige Menge Mathematik] benötigt wird, um diese Operation {{L|Wikipedia:Cross product|richtig zu verstehen}}. | ||
== Rotation == | == Rotation == | ||
Einen Vektor zu rotieren erfordert eine | Einen Vektor zu rotieren erfordert eine {{L|matrix3x4_t|Matrix}}, also kann es nicht mit einer Operation wie oben getan werden. Glücklicherweise muss man nicht in die Details einarbeiten: man kann einfach <code>VectorRotate(Vector in, QAngle in, Vector& out)</code> aufrufen. | ||
== Spezielle Vektoren == | == Spezielle Vektoren == | ||
| Line 114: | Line 114: | ||
=== Länge === | === Länge === | ||
; <code> | ; <code>{{L|vec_t}} Length()</code> | ||
; <code>vec_t LengthSqr()</code> | ; <code>vec_t LengthSqr()</code> | ||
: <code>Length()</code> liefert die Länge des Vektors in | : <code>Length()</code> liefert die Länge des Vektors in {{L|unit|Einheiten}}. Es ist schneller, <code>LengthSqr()</code> zu verwenden und den anderen Vergleichswert zu quadrieren. | ||
; <code> | ; <code>{{L|bool}} IsLengthGreaterThan(flValue)</code> | ||
; <code>bool IsLengthLessThan(flValue)</code> | ; <code>bool IsLengthLessThan(flValue)</code> | ||
: Helfer, die schnelle Längenprüfungen mittels <code>LengthSqr()</code> durchführen. | : Helfer, die schnelle Längenprüfungen mittels <code>LengthSqr()</code> durchführen. | ||
| Line 150: | Line 150: | ||
; <code>Vector2D AsVector2D()</code> | ; <code>Vector2D AsVector2D()</code> | ||
: Castet zu einem | : Castet zu einem {{L|Vector2D}}. | ||
; <code>vec_t Length2D()</code> | ; <code>vec_t Length2D()</code> | ||
; <code>vec_t Length2DSqr()</code> | ; <code>vec_t Length2DSqr()</code> | ||
: Wie die Standardfunktionen, nur dass die Z-Achse ignoriert wird. | : Wie die Standardfunktionen, nur dass die Z-Achse ignoriert wird. | ||
; <code>Base()</code> | ; <code>Base()</code> | ||
: Castet zu einem | : Castet zu einem {{L|vec_t}}* - grundsätzlich das gleiche, wie &vec.x oder (float*)&vec. | ||
== Hilfsfunktionen == | == Hilfsfunktionen == | ||
| Line 161: | Line 161: | ||
Diese globalen Funktionen sind überall über <code>cbase.h</code> verfügbar. | Diese globalen Funktionen sind überall über <code>cbase.h</code> verfügbar. | ||
; <code> | ; <code>{{L|float}} VectorNormalize(vec)</code> | ||
: Teilt den Vektor durch seine Länge - | : Teilt den Vektor durch seine Länge - {{L|normal|normalisiert}} ihn. Passt den Vektor an und liefert die alte Länge. | ||
; <code> | ; <code>{{L|vec_t}} DotProduct(vecA,vecB)</code> | ||
: Siehe [[#Kreuzprodukt|Kreuzprodukt]]. | : Siehe [[#Kreuzprodukt|Kreuzprodukt]]. | ||
; <code>void CrossProduct(vecA,vecB,vecResult)</code> | ; <code>void CrossProduct(vecA,vecB,vecResult)</code> | ||
: Siehe [[#Kreuzprodukt|Kreuzprodukt]]. | : Siehe [[#Kreuzprodukt|Kreuzprodukt]]. | ||
; <code>void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)</code> | ; <code>void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)</code> | ||
: Siehe | : Siehe {{L|matrix3x4_t}}. | ||
* | * {{L|UTIL_VecToYaw()|<code>UTIL_VecToYaw()</code> / <code>UTIL_VecToPitch()</code>}} | ||
* | * {{L|AngleVectors()|<code>AngleVectors()</code> / <code>VectorAngles()</code>}} | ||
== Siehe auch == | == Siehe auch == | ||
* | * {{L|Wikipedia:Euclidean vector}} | ||
* <code> | * <code>{{L|vec_t}}</code> | ||
* <code> | * <code>{{L|Vector2D}}</code> | ||
* <code> | * <code>{{L|QAngle}}</code> | ||
* <code> | * <code>{{L|matrix3x4_t}}</code> | ||
* <code> | * <code>{{L|CUtlVector}}</code> | ||
{{ACategory|Glossary}} | |||
{{ACategory|Variables}} | |||
{{ACategory|Helpers}} | |||
Latest revision as of 02:18, 22 August 2024
Vector ist eine C++-Klasse, die eine Linie mit einer Richtung und einer Länge repräsentiert, die beim aktuellen Ursprung beginnt. Jeder Vektor beinhaltet 3 vec_t Koordinaten:
- X +vorwärts/-rückwärts
- Y +links/-rechts
- Z +oben/-unten
(1,20,5) bedeutet 1 Einheit vorwärts, 20 Einheiten nach links und 5 Einheiten über dem aktuellen Ursprung.
CUtlVector in Source umbenannt.Deklaration
Vector vecMyVector = Vector(1,20,5);
- Der Klassenname
Vectorist Case Sensitive. - Ein Vektor kann erzeugt werden, indem die X-, Y- und Z-Member separat definiert werden, durch das übergeben eines einzelnen Werts für alle 3 oder durch das Kopieren der Daten eines anderen Vektors.
- der Präfix
vec(oder manchmal nurv) identifiziert die Variable als Vektor.
Ausrichtung
Ein Vektor hat keine Ausrichtung; dieser wird durch den Code, der ihn verwendet, bestimmt.
In der überwiegenden Mehrheit der Fälle wird ein Vektor als Weltachsen-ausgerichtet interpretiert, unabhängig von der Ausrichtung der Entity. Es gibt aber ein paar Fälle (z. B. beim Anwenden physikalischer Kräfte), in denen sie als Objektachsen ausgerichtet angesehen werden.
Es gibt keine Möglichkeit, zu sagen, welche Interpretation der Variable verwendet wird, also sollten bei Zweifeln Funktionskommentare zu Rate gezogen werden. Man kann VectorRotate() und VectorIRotate() verwenden, um zwischen den Ausrichtungen zu übersetzen.
Verwendung
- Positionierung
- Jede Position einer Entity ('Ursprung' - "'origin'") wird als Vektor relativ zu seinem übergeordneten Element: wahrscheinlich sind diese bereits als kartesische Koordinaten bekannt. Siehe
GetAbsOrigin()für mehr Details. - Bewegung
- Eine Entity versucht, sich je Sekunde um die Länge seiner Geschwindigkeit zu bewegen.
- Kollisionsspuren
- Eine Traceline oder TraceHull wird von einem Punkt auf einen anderen gefeuert, um aufzuspüren, was es auf seinem Weg trifft.
Operationen
Alle Vektoren müssen innerhalb einer Operation den gleichen Ursprung haben, damit das Ergebnis Sinn ergibt. Ob eine lokaler oder absoluter Ursprung verwendet wird, hängt davon ab, was erreicht werden soll.
Addition
2 (oder mehr) Vektoren zu addieren, kombiniert. Man kennt die Vektoraddition bereits, wenn man ein Objekt mit 2 Händen verschoben hat!
Subtraktion
Einen Vektor von einem anderen abzuziehen erzeugt die Differenz zwischen den beiden - in anderen Worten, wie man zur ersten Position von der zweiten Position kommt. Das Ergebnis ist lokal zum zweiten Vektor.
Multiplikation
Skalar
einen Vektor mit einem Skalar (z. B. ein int oder float) zu multiplizieren oder zu dividieren wird dessen Länge (gelegentlich "Größe" - "magnitude" - genannt), ohne die Richtung zu beeinflussen.
VectorNormalize() verwenden, um dies schnell zu erledigen.Skalarprodukt
Das Multiplizieren zweier Vektoren und addieren der Komponenten des resultierenden Vektors erzeugt ein Skalarprodukt, welches dem Cosinus des Winkels zwischen den Vektoren entspricht, wenn beide Vektoren normalisiert.
Eine Verwendung von Skalarprodukten ist, zu sagen, wie dicht die beiden Vektoren verlaufen. +1 bedeutet, sie stimmen überein, 0 bedeutet, sie stehen senkrecht zueinander und -1 bedeutet, sie sind entgegengesetzt.
Dieser Code berechnet mit der Unterstützung durch die diversen Hilfsfunktionen von Source ein Skalarprodukt:
Vector vecTarget = pTarget->GetAbsOrigin() - GetAbsOrigin(); // Get local vector to target
VectorNormalize(vecTarget); // Normalisierung muss vorher erledigt werden
Vector vecFacing;
AngleVectors(GetLocalAngles(),&vecFacing); // Konvertiert den zugewandten Winkel in einen äquivalenten Vektor
float result = DotProduct(vecTarget,vecFacing); // Das Skalarprodukt errechnen
if (result > 0)
Msg("pTarget ist vor mir!\n");
Kreuzprodukt
Ein Kreuzprodukt ist ein Vektor, der senkrecht zu 2 Eingangsvektoren steht. Er wird verwendet die 3. Dimenson aus nur 2 zu extrapolieren: das Kreuzprodukt eines Vektors, der die X-Achse entlang zeigt und eines Vektors, der die Y-Achse entlang zeigt, ist ein Vektor, der die Z-Achse entlang zeigt.
Die Gleichung ist knifflig und muss nicht gelernt werden; man kann CrossProduct(vecA,vecB,&vecResult) verwenden. Es besteht grundsätzlich keine Notwendigkeit, die Eingabevektoren zu normalisieren. Die meisten Modder werden Kreuzprodukte nur selten verwenden, wenn überhaupt. Wenn jedoch benötigt, dass eine mäßige Menge Mathematik benötigt wird, um diese Operation richtig zu verstehen.
Rotation
Einen Vektor zu rotieren erfordert eine Matrix, also kann es nicht mit einer Operation wie oben getan werden. Glücklicherweise muss man nicht in die Details einarbeiten: man kann einfach VectorRotate(Vector in, QAngle in, Vector& out) aufrufen.
Spezielle Vektoren
Source definiert 2 spezielle Vektoren:
vec3_origin- Vector(0,0,0).
vec3_invalid- Dieser wird für ungültige Vektoren verwendet, z. B. wenn eine Funktion einen Vektor zurückliefern soll, dies aber nicht möglich ist (beispielsweise der Schnittpunkt zweier paralleler Linien).
Memberfunktionen
Länge
vec_t Length()vec_t LengthSqr()Length()liefert die Länge des Vektors in Einheiten. Es ist schneller,LengthSqr()zu verwenden und den anderen Vergleichswert zu quadrieren.bool IsLengthGreaterThan(flValue)bool IsLengthLessThan(flValue)- Helfer, die schnelle Längenprüfungen mittels
LengthSqr()durchführen. void Zero()- Setzt alle Elemente auf 0.
Richtung
void Init(vec_t X, Y, Z)- Schnelles setzten der Komponenten eines Vektors.
void Random(vec_t minVal,vec_t maxVal)- Wählt zufällig neue Werte für die 3 Komponenten innerhalb des gegebenen Bereichs.
void Negate()- Kehrt die Richtung eines Vektors um, ohne die Länge zu beeinflussen.
Vector Max(vOther)Vector Min(vOther)- Schneidet die Komponenten ab, sollten sie sich über oder unter dem angegebenen Wert befinden. Die Komponenten behalten dabei nicht ihre Proportionen (die Richtung ändert sich möglicherweise).
Vergleich
vec_t DistTo(vOther)vec_t DistToSqr(vOther)- Liefert die Distanz zwischen dem aktuellen Vektor und
vOtherals Skalar. Wie immer ist das quadrierte Ergebnis schneller. vec_t Dot(vOther)- Liefert das Skalarprodukt des aktuellen Vektors und
vOther. Vector Cross(vOther)- Liefert das Kreuzprodukt des aktuellen Vektors und
vOther. bool WithinAABox(vecBoxmin,vecBoxmax)- Prüft, ob der Vektor innerhalb der gegebenen Box endet. Boxmin und -max sind lokal zum Vektor.
Casts
Vector2D AsVector2D()- Castet zu einem Vector2D.
vec_t Length2D()vec_t Length2DSqr()- Wie die Standardfunktionen, nur dass die Z-Achse ignoriert wird.
Base()- Castet zu einem vec_t* - grundsätzlich das gleiche, wie &vec.x oder (float*)&vec.
Hilfsfunktionen
Diese globalen Funktionen sind überall über cbase.h verfügbar.
float VectorNormalize(vec)- Teilt den Vektor durch seine Länge - normalisiert ihn. Passt den Vektor an und liefert die alte Länge.
vec_t DotProduct(vecA,vecB)- Siehe Kreuzprodukt.
void CrossProduct(vecA,vecB,vecResult)- Siehe Kreuzprodukt.
void VectorTransform(Vector in1, matrix3x4_t in2, Vector out)- Siehe matrix3x4_t.