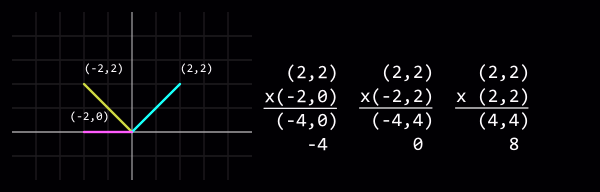User:TomEdwards/Vector draft
Vector is a C++ class that represents a line with direction and length, starting at the current origin.
Each vector contains three vec_t 'ordinates'. (0,20,5) is a Vector that ends 20 units in front and 5 units above the current origin.
Note:Source's vector class is very different to the Standard Template Library's, which is a type of array. The STL-style vector has been renamed CUtlVector in Source.Declaration
Vector vecMyVector = Vector(0,20,5);
You could also assign to the X, Y and Z member variables separately.
Uses
Positioning
Every entity's position is stored as a vector relative to its parent. You are likely to be familiar with this idea already as grid coordinates.
The parent-relative vector stored by the entity is 'local'; calculating an 'absolute' vector relative to the world requires extra work. The two Abs functions below do that work for you, but are more expensive.
Movement
An entity attempts to move the length of its velocity vector once per second. The movement code looks something like this:
Vector velocity = Vector(0,5,0); // 5 units/second forward Vector vecNewOrigin = GetAbsOrigin() + velocity * gpGlobals->frametime; // frametime is in seconds, e.g. 0.033 SetAbsOrigin(vecNewOrigin);</source>
Notice how frametime is used to regulate the entity's speed regardless of how long each frame takes to calculate. See scalar multiplication for more detail on the operation.
As with the origin, velocity is stored relative to the entity.
Tracelines
Operations
Addition
Adding two (or more) vectors combines them. You have already experienced vector addition if you've ever pushed an object with two hands!
Subtraction
Subtracting one vector from another produces the difference between the two - in other words, how to get to the first location from the second.
Tip:The order in which you subtract defines the direction of the vector.Multiplication
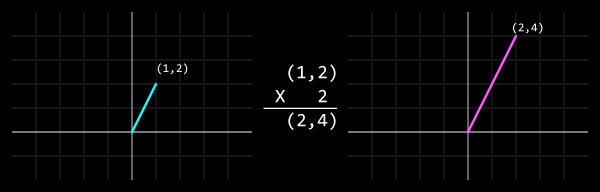
Scalar
Multiplying or dividing a vector by a scalar (i.e. an int or float) will change its length (sometimes called "magnitude") without affecting its direction.
Tip:Dividing a vector by its length normalises it. Use VectorNormalize() to do this quickly.Dot product
Multiplying two normalised (see above) vectors then adding the result's ordinates produces a dot product, which tells you how closely the direction of two vectors match. +1 means a match, 0 means they are perpendicular to each other, and -1 means they are opposed.
Note:True dot products are only produced when the length of both vectors is 1. The normalisation step has been skipped in the following demonstration to make its equations simpler (but the positive/zero/negative rule still applies).
This code calculates a dot product with the aid of Source's various helper functions:
Vector vecTarget = GetAbsOrigin() - pTarget->GetAbsOrigin(); // Get target's direction VectorNormalize(vecTarget); // Length now equals 1 Vector vecFacing; AngleVectors( GetLocalAngles(), &vecFacing ); // Convert facing angle to equivalent vector (arrives normalised) float result = DotProduct(vecTarget,vecFacing); // Get the dot product! This function won't itself normalise if (result >0) Msg("pTarget is in front of me!\n");
Tip:There is no need to normalise if you only care about whether one location is in front of another.Cross product
A cross product is a vector perpendicular to two input vectors used to extrapolate an axis in the third dimension. The equation is fiddly and doesn't have to be learnt; just use CrossProduct(). There generally isn't any need to normalise the input vectors.
Cross products as a concept can't easily be demonstrated in two dimensions, but consider this: the cross product of a vector pointing down the X-axis and a vector pointing down the Y-axis is a vector pointing down the Z-axis.
Member functions
float/vec_t Length()vec_t VectorLength(const Vector&)- Returns the vector's length, in units.
vec_t LengthSqr()- Returns length squared.
vec_t Length2D()vec_t Length2DSqr()- Todo: ???
void Negate()- Reverses the vector's direction without affecting its length.
vec_t DotProduct(const Vector& a, const Vector& b)- Todo: Someting to do with determining how closely two vectors match.
void CrossProduct(const Vector& a, const Vector& b, Vector& result )- Todo: Something to do with creating a surface normal.
bool WithinAABox( Vector const &boxmin, Vector const &boxmax)- Does the Vector intersect this axis-aligned box? Todo: Are argument vectors local or abs?